We are going to study FSc Part 1 Chapter 3 Chemistry with the help of notes and quizzes. By preparing this you can produce outstanding results in exams.
Attempt MCQ quiz 1 (Past Papers) To main menu⏫
Attempt MCQ quiz 2 (Entrance Test Questions) To main menu⏫
Video lectures of the same chapter (FSc part 1 chapter 3 Chemistry) are already been uploaded on YouTube at Umair khan Academy in Urdu/Hindi. You can also jump right now to the class 11 website page which is managed according to your ease. To main menu⏫
Questions-Answers and Notes for FSc part 1 chapter 3 Chemistry To main menu⏫
Boyle’s Law
Q.1 Why does Boyle’s law apply only to the ideal gases
Boyle’s law applies to those gases which have no forces of attraction among the molecules. Such gases are ideal. So, Boyle’s law applies to only ideal gases.
Q.2 What is an isotherm
Isotherms are the graph between pressure and volume at constant temperature and number of moles this condition is fulfilled by Boyle’s law. The word isotherm means the same temperature.
Q.3 What are isotherms? What happens to the positions of isotherms when they are plotted at high temperatures for a particular gas
Isotherms are the graphs between pressure and volume when the temperature is constant. These graphs are plotted to keep in view Boyle’s Law. When the isotherms are plotted at higher temperatures, then they go away from the axis. The reason is that the volumes of the gases increase at high temperatures.
Q.4 The product of pressure and volume at constant temperature and the number of moles is a constant quantity. Why
When the temperature and number of moles of gas are constant, then the increase of pressure decreases the volume in such a way that PV remains constant (PV=K). By doubling the pressure, the volume becomes half. We can say that, P₁V₁= P₂V₂= P3V3, at constant temperature and number of moles.
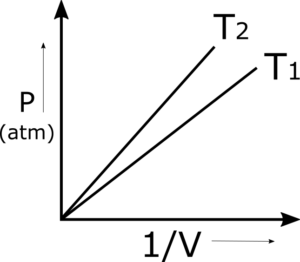
Q.5 Why do we get a straight line when pressures are plotted against the inverse of volumes? This straight line changes its position in the graph by varying the temperature. Justify it
When the pressure of a gas is plotted against 1/V, we get a straight line at a constant temperature. The reason is that P and 1/V are directly proportional to each other. Simply, when P (pressure) increases then volume decreases at a constant temperature, as 1/V is the inverse of V (volume) so it should be directly proportional to P and results in a straight line.
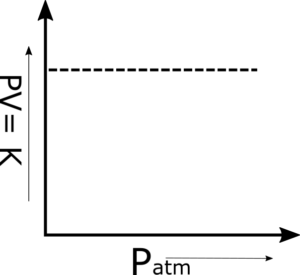
Q.6 The plot of PV versus P is a straight line at constant temperature and with a fixed number of moles of an ideal gas. Why?
The product PV is a constant quantity when temperature and the number of moles are constant. So, when we plot a graph between pressure on the x-axis and PV on the y-axis, then a straight line parallel to the pressure axis is obtained. This is a verification of Boyle’s Law.
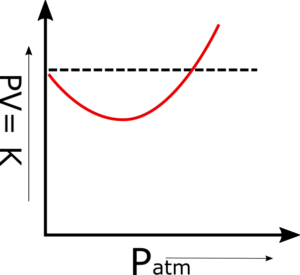
Q.7 How do you explain that the value of the constant k in (PV= k) in Boyle’s law depends upon (i) The temperature of a gas (ii) the quantity of gas
(i) In Boyle’s law, the temperature is kept constant for a fixed number of moles of an ideal gas. So the product PV remains constant. Anyhow, if the temperature of the gas is increased, then the volume increases for the same number of moles. So the product PV increases. Anyhow, if the increase of temperature is carried out by keeping the volume constant, then the pressure increases for the same amount of gas. So the product PV increases. Similarly, by decreasing the temperature the product PV decreases.
(ii). When the quantity of gas is increased at the same temperature, then the volume increases and so the product PV increases.
Q.8 Why does the straight line parallel to the x-axis in a graph, PV vs P, goes away from the pressure axis at higher pressures. Why?
When the pressure on the gases is increased beyond certain limits, then PV versus P is no more a straight line parallel to the pressure axis. The straight line becomes a curve depending upon the nature of the gas. In this situation, gases become non-ideal.
Q.9 What are various units of pressure
1 atm = 760 mm Hg = 760 torr = 101325 Nm-2 = 101325 Pa = 101.325 kp = 1.01325 Bar = 14.7 pounds Inch-1
Q.10 Greater the temperature of the gas closer to the straight line of P versus 1 to the pressure axis. Justify it
When the temperature of the same gas is increased for the same number of moles, then the volumes increase at the same pressure. The inverse of volume decreases at the same pressure. So the points for the graph lie above the lower temperature graph.
Charles’s Law
Q.11 Charles’s law is not obeyed when the temperature is measured on the Celsius scale. Justify it
The foundation stone of Charles’s law is the absolute scale of temperature which starts from -273°C. The volume of the gas at any temperature can be calculated from the equation
VT = Vo (1+T/273)
Hence, V1/T1 = V2/T2 is only obeyed, if the temperature is substituted in absolute scale.
Q.12 What is absolute zero? What happens to real gases while approaching them
It is the lowest possible temperature which would have been achieved if the substance remains in the gaseous state. All the real gases are converted to liquids above this temperature. This -273.16°C is called zero absolute or zero Kelvin.
Q.13 A gas occupies 100 dm3 at 283 K. What will be its volume at – 273°C at constant pressure?
Ans: All the gases are converted into the liquid state before reaching -273°C. It means that the concerned gas is liquid at -273°C, so the volume of this gas at -273°C cannot be predicted.
Q.14 Throw some light on the factor 1/273 in Charles’s law
The factor of 1/273 is very important in Charles’s law. The volume of a given mass of the gas increases or decreases by 1/273 of its volume at 0°C. The following equation helps us to calculate the volume of gas at any temperature.
VT = V0(1 + T/273)
Q.15 Justify that the volume of a given mass of gas becomes theoretically zero at -273°C.
According to Charles’s law, the volume of a given mass of the gas at 0°C increases or decreases by 1/273 of its original volume, when the temperature is increased or decreased by 1°C.
In VT = V0(1 + T/273) putting the values T = -273 oC and you will get answer zero.
Q.16 How do you explain that -273°C is theoretical temperature and is not attainable
Gases become liquids before reaching -273°C. Hence -273°C is not an attainable temperature. We reach this temperature theoretically. If the volume of gas would have been zero in the laboratory at -273°C, then the law of conservation of mass would have been violated.
Q.17 What are various scales of thermometry? Convert 80°C to Fahrenheit
There are three scales of thermometry, i.e. Centigrade, Fahrenheit and Absolute or Kelvin scale.
- K = (°C+273)
- °C =5/9 (F-32)
- F = 9/5(°C) +32
Solution
- F = 9/5(°C) +32
- F= 9/5 x 80 +32
- F = 144 +32
- F=176 °
General Gas Constant
Q.18 How the value of the general gas constant ‘R’ can be derived with the help of Avogadro’s law
According to Avogadro’s law, the volume of one mole of all the ideal gases at S.T.P. is 22.414 dm³. Putting the values of P, T, V and n, the value of R.
R = PV/nT = 1 atm x 22.4 dm³/ 1 mole x 273.16 K = 0.0821 dm³ atm K-1 mol-1.
Q.19 Calculate the S.I. unit of R
According to Avogadro’s law, we put the values of P = 101325, V=0.022414 m3 and T = 273.16 K
R = PV/ nT = 101325 Nm-2x 0.022414 m³/1 mole x 273.16 K = 8.3143 JK-1 mol-1.
Q.20 How does the density of an ideal gas double by doubling the pressure or decreasing the temperature on the Kelvin scale by 1/2
We know that d =PM/RT When the pressure is doubled the density should be doubled according to the above equation. Similarly, when the temperature becomes half, the density is also doubled. It can also be represented as d = 2 PM/RT And d = PM/R ( T/2)
Avogadro’s Law
Q.21 What is Avogadro’s law of gasses
Equal volumes of all the gases at the same temperature and pressure, contain an equal number of molecules.
Q.22 Justify that 1cm³ of H₂ and 1 cm³ of CH4 at STP will have the same number of molecules. When one molecule of CH4 is 8 times heavier than hydrogen
According to Avogadro’s law, equal volumes of all the ideal gases at the same temperature and pressure have equal numbers of molecules. So 1 cm³ of H2 and 1 1 cm³ of CH4 at STP will have an equal number of molecules. No doubt, the molecule of methane is eight times heavier than H₂, but the sizes of the gas molecules and their masses don’t disturb the volumes. The reason is that at STP, one molecule of the gas is at a distance of three hundred times greater than its diameter.
Dalton’s law of partial pressures
Q.23 Why do pilots feel uncomfortable breathing at high altitudes
It is due to the low partial pressure of O₂ in the upper atmosphere. The pressure inside the lungs is greater than the partial pressure of O₂ in the air.
Q.24 State Dalton’s law of partial pressures. Give its expression
The total pressure exerted by the mixture of gases is equal to the sum of individual partial pressures at a given temperature. Let there be a mixture of three gases
P= PH₂ + PO₂+ PCH4
P = nt RT/V where nt = nH₂ + no₂+ nCH4
Q.25 How do you say that the pressure of the dry gas is equal to the difference between total pressure and aqueous tension of H₂O?
Some gases prepared in the laboratory are to be collected over water. So, water vapour joins the gas. To get the pressure of the real gas, we have to subtract the vapour pressure of water (aqueous tension) from the total pressure.
- Pt = Pgas + aqueous tension
- Pgas = Pt – aqueous tension
Graham’s Law of Diffusion
Q.26 Lighter gases diffuse more rapidly than heavier gases. Give reason.
At a given temperature the average K.E. of different gas molecules is the same. Since their masses are different, so their velocities will also be different. The lighter molecules will have greater velocities and so they will diffuse rapidly.
Non-ideal Behaviour of Gases
Q. 27 Gases deviate more from the general gas equation at 0°C and deviate to less extent at 100°C. Why
At 0°C, the forces of attraction are dominant and gases become non-ideal. At high temperatures, attractive forces become less dominant and gases behave ideally.
Q.28. The actual volume of O2 gas at room temperature and 1 atm. pressure is negligible as compared to the volume occupied by one mole of this gas. But this actual volume is not negligible at high pressures. Justify it.
At ordinary temperature and pressure, there are almost no forces of attraction among the molecules of O₂. The actual volume of the gas molecules is negligible as compared to the volume of the vessel. When the pressure is increased for O₂, then molecules come close to each other. Collisions become more frequent. Forces of attraction start dominating. Actual volume remains no longer negligible.
Q.29 Hydrogen and helium are ideal at room temperature, but SO₂ and Cl₂ are non-ideal. How do you explain it?
H₂ and He have very low boiling points. So at room temperature, they are far away from their boiling points. At room temperature, the attractive forces are absent. So they behave ideally.
SO₂ and Cl₂ have boiling points close to room temperature but are below 0°C. At room temperature, they are not far away from their boiling points. Sufficient attractive forces are present at room temperature. So they are non-ideal.
Liquefaction of Gases
Q.30 How is the critical temperature is an essential criterion to be considered for the liquefaction of gases
Gases can be liquefied by increasing the pressure and decreasing the temperature. The temperature of gas should reach the critical temperature on or below that to make the gas into a liquid. Gas can never be liquefied whether how much pressure is applied if the gas is above the critical temperature.
Q.31 Why do non-polar gases like H2, and He have a very low critical temperature while polar gases like NH3 and SO2 have critical temperatures sufficiently above room temperature
H₂ and He are consist of small-sized molecules and have low polarizabilities. They have fewer forces of attraction among themselves. To liquefy them, their temperatures have to bring close to absolute zero. NH3 and SO2 have attractive forces even at room temperature. To liquefy them, their temperature may be above room temperature.
Q.32 In the Joule-Thomson effect sudden expansion of the gas molecules needs energy. Why
In the compressed state, there are sufficient attractive forces among the molecules of the gas. During sudden expansion, energy is required to overcome the intermolecular attractions. Moreover, the molecules need extra energy to run away in a vacuum.
Q.33 The Joule-Thomson effect is operative in Linde’s method of liquefaction of air. How?
In Linde’s method, the gas is compressed to 200 atmospheric pressure. These compressed gases are suddenly allowed to expand through a nozzle. This sudden expansion of the gas and the consequent cooling is called the Joule-Thomson effect and this effect is operative in Linde’s method of liquefaction.
Non-ideal Behaviour of Gases
Q.34 Why do the gases deviate from ideal behaviour at high pressure and low temperature
When the temperature of the gases is low, the attractive forces become dominant, so gases don’t obey the gas laws. When the pressure of the gases is high, collisions become more frequent and forces of attraction are created. Moreover, the actual volume of the gas molecules is no more negligible as compared to the volume of the vessels.
Q.35 Water vapours do not behave ideally at 273 K. Why
When water vapours are present at 273 K (0 C°), there are sufficient forces of attraction among its molecules at 0°C (freezing point of water). Due to this reason, water vapours behave non-ideally at 273 K.
Q.36 Give two causes for the deviation of gases from ideality
The causes are due to two faulty assumptions:
- The actual volume of the gas molecules is negligible as compared to the volume of the vessel.
- There are no forces of attraction among the molecules of gases.
These two postulates are correct when the temperature is high or the pressure is low.
Q.37 SO₂ is comparatively non-ideal at 273 K but behaves ideally at 327 K
SO2 gas is close to its boiling point at 273 K. So, at 273 K, attractive forces are dominating and make the gas non-ideal. But when the temperature of the gas is high as 327 K, then forces of attraction are less dominant and the gas behaves ideally.
Van der Waal’s Equation
Q.38 How the behaviour of real gases is given by van der Waal’s equation?
The constants ‘a’ and ‘b’ are called van der Waal’s constants give the quantitative measurements of attractive forces and sizes of the gas molecules. These parameters are very important for real gases.
Q.39 Why the pressure correction is done by van der Waal
The pressure is exerted due to collisions on the walls of the vessel. Attractive forces decrease the intensity of collisions. So the observed pressure on the walls is less than the ideal pressure. Lessened pressure is added in observed pressure to get ideal pressure.
Q.40 Why the volume correction is done by van der Wall?
The molecules of a gas do occupy a certain volume, which is not available to the gas molecules in the vessel. This is called excluded volume and should be subtracted from the volume of the vessel to get the free volume available to gas molecules.
Vfree = Vvessel-b
Q.41 Why the excluded volume is less than the molar volume of the gas
Excluded volume ‘b’ is the volume of one mole of the real gas in the highly compressed state. But molar volume (Vm) is that volume when the same gas is liquefied and molecules are touching each other every moment. So,
b = 4 Vm
Q.42 Why some amount of pressure should be added to the measured pressure of the non-ideal gas to get the ideal pressure of the gas?
The forces of attraction of nearby molecules of gases decrease the observed pressure (P) by (P’) while colliding the walls of the vessel and actual pressure (Pi) can’t be measured. Therefore, P’ should be added to the observed pressure (P) to get actual true pressure.
Pi = P+P’
Q.43 Pressure of NH3 gas at given conditions (say 20 atm pressure and room temperature) is less when calculated by Van der Wall’s equation than that calculated by the general gas equation. Why
NH3 is a polar gas and has forces of attraction in its molecules when the pressure is high. It shows non-ideal behaviour at high pressures. The factors ‘a’ and ‘b’ become dominant at this pressure and van der Waal’s equation gives less pressure than that calculated by the general gas equation.
Q.44 What is the physical significance of van der Wall’s constants, ‘a’ and ‘b’. Give their units. Van der Waal has modified the general gas equation
(P+ a/V2) (V-b) = RT (van der Waal’s equation for one mole of gas)
The factor ‘a’ is for the attractive forces present among the molecules of the gas. The greater the polarity of gas, the greater the attractive forces, the greater the ‘a’ factor. Its units are atm.dm6. mol-2.
The factor ‘b’ is related to the volume of gas molecules which they occupy in the vessel and that volume is not available to the gaseous molecules. This is called excluded volume and has the units of dm3mole-1
Plasma State
Q.45 What are the characteristics of plasma?
The motions of particles in the plasma generate fields and electrical currents from within plasma density. In this way, the plasma is a uniquely fascinating and complex state of matter. The plasma is neutral overall.
Q.46 Where is plasma found?
It is the most abundant form of matter in the universe. It is the stuff of stars. Our sun is a 1.5 million km ball of plasma. On Earth, it occurs in lightning bolts, flames, auroras and fluorescent tubes.
Q.47 What are the applications of plasma
- Glowing plasma inside the bulb
- Neon signs
- Processing of semi-conductors
- Sterilization of medical products.



